Package Summary
| Tags | No category tags. |
| Version | 0.0.1 |
| License | MIT |
| Build type | CMAKE |
| Use | RECOMMENDED |
Repository Summary
| Description | Lie theory for robotics |
| Checkout URI | https://github.com/pettni/smooth.git |
| VCS Type | git |
| VCS Version | master |
| Last Updated | 2024-10-18 |
| Dev Status | UNMAINTAINED |
| CI status | No Continuous Integration |
| Released | UNRELEASED |
| Tags | cpp robotics eigen header-only lie-groups cpp20 lie-algebra |
| Contributing |
Help Wanted (0)
Good First Issues (0) Pull Requests to Review (0) |
Package Description
Additional Links
Maintainers
- Petter Nilsson
Authors
- Petter Nilsson
Lie Theory for Robotics
- Requirements: C++20, Eigen 3.4
- Documentation
- Compatible with: autodiff, boost::numeric::odeint, Ceres, ROS
- Written in an extensible functional programming style
In robotics it is often convenient to work in non-Euclidean manifolds. Lie groups are a class of manifolds that are easy to work with due to their symmetries, and that are also good models for many robotic systems. This header-only C++20 library facilitates leveraging Lie theory in robotics software, by enabling:
- Algebraic manipulation
- Automatic differentiation
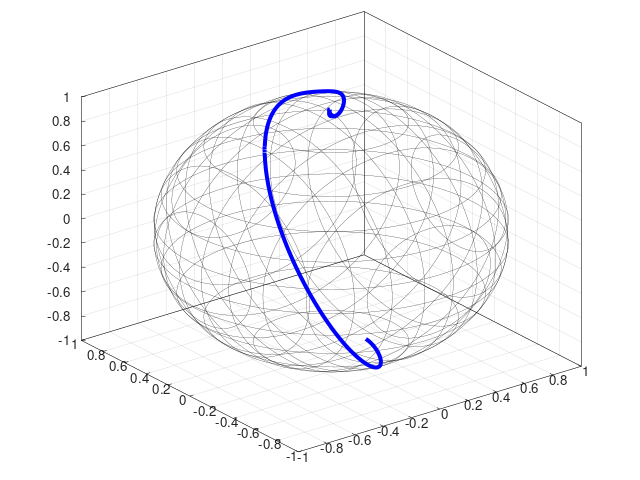
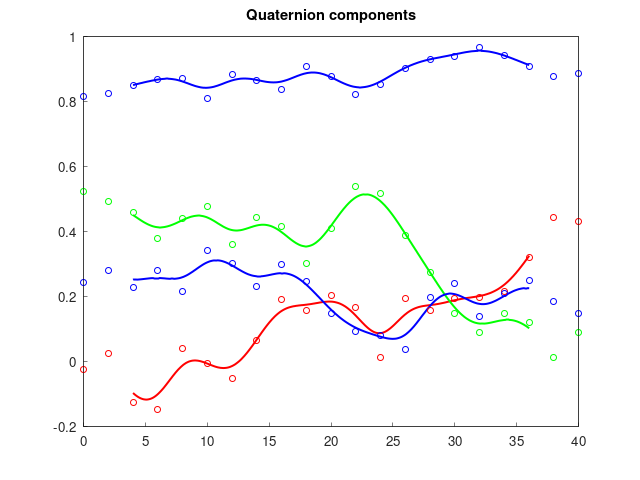
- Interpolation (right figure shows a B-spline of order 5 on smooth::SO3, see
examples/bspline.cpp) - Numerical integration (left figure shows the solution of an ODE on
, see
examples/odeint.cpp) - Optimization
The following common Lie groups are implemented:
- smooth::SO2: two-dimensional rotations with complex number
memory representation
- smooth::SO3: three-dimensional rotations with quaternion
memory representation
- smooth::SE2: two-dimensional rigid motions
- smooth::SE3: three-dimensional rigid motions
- smooth::C1: complex numbers (excluding zero) under multiplication
- smooth::Galilei: the Galilean group. It includes SE_2(3) as a special case.
- smooth::SE_K_3: generalization of SE3 with multiple translations
- A smooth::Bundle type to treat Lie group products
as a single Lie group. The Bundle type also supports regular Eigen vectors as
components
- Lie group interfaces for Eigen vectors and builtin scalars
Getting started
Download and Build
Clone the repository and install it
git clone https://github.com/pettni/smooth.git
cd smooth
mkdir build && cd build
# Specify a C++20-compatible compiler if your default does not support C++20.
# Build tests and/or examples as desired.
cmake .. -DBUILD_EXAMPLES=OFF -DBUILD_TESTS=OFF
make -j8
sudo make install
Alternatively, if using ROS or ROS2 just clone smooth into a
catkin/colcon workspace source folder and build the
workspace with a compiler that supports C++20. Example with colcon:
colcon build --cmake-args -DCMAKE_CXX_COMPILER=/usr/bin/g++-10
Use with cmake
To utilize smooth in your own project, include something along these lines in your CMakeLists.txt
find_package(smooth)
add_executable(my_executable main.cpp)
target_link_libraries(my_executable smooth::smooth)
Explore the API
Check out the Documentation and the examples.
Using the library
Algebraic Manipulations
// Also works with other types: SO2d, SE2d, SE3d, Bundle<SO3d, T3d> etc...
using Tangent = typename smooth::SO3d::Tangent;
// construct a random group element and a random tangent element
smooth::SO3d g = smooth::SO3d::Random();
Tangent a = Tangent::Random();
// lie group exponential
auto exp_a = smooth::SO3d::exp(a);
// lie group logarithm
auto g_log = g.log();
// lie algebra hat and vee maps
auto a_hat = smooth::SO3d::hat(a);
auto a_hat_vee = smooth::SO3d::vee(a_hat);
// group adjoint
auto Ad_g = g.Ad();
// lie algebra adjoint
auto ad_a = smooth::SO3d::ad(a);
// derivatives of the exponential map
auto dr_exp_v = smooth::SO3d::dr_exp(a); // right derivative
auto dl_exp_v = smooth::SO3d::dl_exp(a); // left derivative
auto dr_expinv_v = smooth::SO3d::dr_expinv(a); // inverse of right derivative
auto dl_expinv_v = smooth::SO3d::dl_expinv(a); // inverse of left derivative
// group action
Eigen::Vector3d v = Eigen::Vector3d::Random();
auto v_transformed = g * v;
// memory mapping using Eigen::Map
std::array<double, smooth::SO3d::RepSize> mem;
Eigen::Map<const smooth::SO3d> m_g(mem.data());
Concepts and Types
These C++20 concepts are implemented in concepts.hpp.
-
Manifold: type for whichrplus(geodesic addition) andrminus(geodesic subtraction) are defined. Examples:- All
LieGrouptypes -
std::vector<Manifold>is a Manifold defined inmanifold_vector.hpp—it facilitates e.g. optimization and differentiation w.r.t. a dynamic number ofManifolds -
std::variant<Manifold ...>is a Manifold defined inmanifold_variant.hpp. Usingstd::vector<std::variant<Manifold...>>can be convenient when optimizing over variables with different parameterizations.
- All
-
LieGroup: type for which Lie group operations (exp,log,Ad, etc…) are defined. Examples:- All
NativeLieGrouptypes - Fixed-size Eigen vectors (e.g.
Eigen::Vector3d) - Dynamic-size Eigen vectors (e.g.
Eigen::VectorXd) - Built-in scalars (e.g.
double)
- All
-
NativeLieGroup: type that implements the Lie group operations as class methods. Examples:smooth::SO3<float>smooth::C1<double>smooth::Bundle<NativeLieGroup | Eigen::Matrix<Scalar, N, 1> ...>
Both Manifold and LieGroup are defined via external type traits (traits::man and traits::lie) that can be specialized in order to define Manifold or LieGroup interfaces for third-party types.
Algorithms
Tangent space differentiation
Available for Manifold types, see diff.hpp.
Supported techniques (see smooth::diff::Type):
- Numerical derivatives (default)
- Automatic differentiation using
autodiff(must #include <smooth/compat/autodiff.hpp>) - Automatic differentiation using Ceres 2.x (must #include <smooth/compat/ceres.hpp>)
Example: calculate for i=1, 2
#include <smooth/diff.hpp>
#include <smooth/so3.hpp>
auto f = []<typename T>(const smooth::SO3<T> & v1, const smooth::SO3<T> & v2) {
return (v1 * v2).log();
};
smooth::SO3d g1 = smooth::SO3d::Random();
smooth::SO3d g2 = smooth::SO3d::Random();
// differentiate f at (g1, g2) w.r.t. first argument
auto [fval1, J1] = smooth::diff::dr<1>(f, smooth::wrt(g1, g2), std::index_sequence<0>{});
// differentiate f at (g1, g2) w.r.t. second argument
auto [fval2, J2] = smooth::diff::dr<1>(f, smooth::wrt(g1, g2), std::index_sequence<1>{});
// differentiate f at (g1, g2) w.r.t. both arguments
auto [fval, J] = smooth::diff::dr<1>(f, smooth::wrt(g1, g2));
// Now J == [J1, J2]
Non-linear least squares optimization
Available for Manifold types, see optim.hpp.
The minimize() function implements a Levenberg-Marquardt trust-region procedure to find a local minimum. All derivatives and computations are done in the tangent space as opposed to e.g. Ceres which uses derivatives w.r.t. the parameterization.
A sparse solver is implemented, but it is currently only available when analytical derivatives are provided.
| Example: Calculate &space;| | ) |
#include <smooth/optim.hpp>
#include <smooth/so3.hpp>
smooth::SO3d g1 = smooth::SO3d::Random();
const smooth::SO3d g2 = smooth::SO3d::Random();
// function defining residual
auto f = [&g2]<typename T>(const smooth::SO3<T> & v1) {
return (v1 * g2.template cast<T>()).log();
};
// minimize || f ||^2 w.r.t. g1 (g1 is modified in-place)
smooth::minimize(f, smooth::wrt(g1));
// Now g1 == g2.inverse()
Piecewise polynomial curve evaluation and fitting
Available for LieGroup types, see spline/spline.hpp.
These splines are piecewise defined via Bernstein polynomials and pass through the control points. See examples/spline_fit.cpp for usage.
B-spline evaluation and fitting
Available for LieGroup types, see spline/bspline.hpp.
The B-spline basis functions have local support, A B-spline generally does not pass through its control points. See examples/spline_fit.cpp and examples/bspline.cpp for usage.
Compatibility
Utility headers for interfacing with adjacent software are included.
- compat/autodiff.hpp: Use the autodiff library as a back-end for automatic differentiation
- compat/ceres.hpp: Local parameterization for Ceres on-manifold optimization, and use the Ceres automatic differentiation as a back-end
- compat/odeint.hpp: Numerical integration using
boost::odeint - compat/ros.hpp: Memory mapping of ROS/ROS2 message types
Related Projects
-
smooth_feedback utilizes
smoothfor control and estimation on Lie groups.
Two projects that have served as inspiration for smooth are manif—which
also has an accompanying paper that is a great practical introduction to
Lie theory—and Sophus. Certain design decisions are different in
smooth: derivatives are with respect to tangent elements as in manif, but the tangent
types are Eigen vectors like in Sophus. This library also includes the Bundle type which
facilitates control and estimation tasks, as well as utilities such as differentiation,
optimization, and splines. Finally smooth is written in C++20 and leverages modern
features such as concepts and
ranges.
Wiki Tutorials
Dependant Packages
| Name | Deps |
|---|---|
| smooth_feedback |



